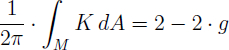Home

Begrüßung

Willkommen auf meiner Homepage! Mein Name ist: Sven Dooley. Diese Internetpräsenz ist mit dem Browser „Mozilla Firefox“ mit der Bildschirmauflösung 1920×1080 am besten zu betrachten. Unten sollte ein Video abgespielt werden. Falls nicht, drücken Sie, wenn Sie natürlich wollen, auf das Video, um es abzuspielen. Sollte das Video jedoch automatisch gestartet haben und Sie stören, dann bewegen Sie bitte den Mauszeiger auf das Video, um auf Pause zu stellen. Viel Spaß!

Das folgende Video ist das Video zu meiner Homepage! „Surfer“ trifft eine Entscheidung, wie er als Todkranker verschwinden kann, um nicht als Last zu enden. Er entscheidet jetzt aus der Formation auszubrechen, indem er seinen Steuerknüppel nach links ausschlägt:

Mein Rufname

Jeder Kampfjetpilot hat einen sogenannten Rufnamen. Obwohl ich kein Pilot bin, habe ich mir einen Rufnamen zugeordnet. Mein Rufname ist „Eagleeye“. Dass ich mir einen solchen zuordne, kommt daher, dass ich Kampfjets gut finde.

Hier sind nun noch fünf Videos, die mir als Kampfpilot, der bei Falcon 4.0 (Kampfflugsimulator) Kampfeinsätze geflogen ist, aus der Serie „Pensacola - Flügel aus Stahl“ am Herzen liegen. Ich wünsche viel Spaß am Kämpferdasein der Kampfpiloten!

Schöne Mathematik

Mathematik ist eine exakte Naturwissenschaft, die vieles sehr gut kann: Sie löst schwierigste Probleme aus der Natur, die meiner Meinung nach in den Formeln der Logik geschrieben ist, derer sich die Mathematik bedient, so dass man etwas sehr Wichtiges bekommt, wie Erkenntnis, Wissen und Fortschritt, z.B. in der Technik oder in anderen Naturwissenschaften, wie z.B. Informatik, Physik, Chemie oder auch Biologie. Es ergeben sich daraus wichtige Anwendungsmöglichkeiten etwa aus Methoden, Strukturen, Algorithmen, Kalkulationen, Modelle und Theorien. Ein weiteres Merkmal der Mathematik ist, dass sie eine exakte, präzise und korrekte Sprache ist, die Phänomene in der Natur beschreiben kann, damit man ganz genau weiß, worüber man spricht. In der Mathematik geht es um das logische Denken, man will Aussagen über Zahlen, Figuren und Strukturen finden, die alle beweisen und mit Kombinieren neue Aussagen ableiten, um die Theorie zu vervollständigen. Konkret kann Mathematik z.B. lineare Gleichungssysteme, die Bedingungen eines Informationssystems repräsentieren können, systematisch lösen, Differentialgleichungen, die dynamische Prozesse in der Natur beschreiben, auflösen, man kann dort aber auch z.B. den Flächeninhalt einer einigermaßen beliebig geformten Fläche im Raum ausrechnen, auch ist es möglich Aussagen über die Konstruierbarkeit gewisser geometrischer Objekte mit Zirkel- und Linealkonstruktionen zu machen und man hat die Befähigung in einem Kantennetz von einem Punkt zu einem anderen den Weg minimaler Summe von Kantenbewertungen zu finden. Und es gibt noch vieles mehr, was die Mathematik so alles kann. Und jetzt etwas für das Auge:

Meine Meinung als Theoretiker: Alles ist Zusammenhang, Logik, Gesetze, System und Struktur! Und es bedeutet Macht, wenn man mit der Brille eines Theoretikers auf die Welt alles Konstruiertem im Universum zugreifen kann! Man findet heraus, wie die Welt funktioniert und man kann sich Erkenntnisse zu Nutze machen. Die Philosophie der messerscharf denkenden Theoretiker lautet folgendermaßen: WENN ES LOGISCH IST, DANN PASST ES!

Das logisch-analytische Denken, welches in der höheren Mathematik jede Sekunde pur vollzogen wird, fußt grundsätzlich auf drei Säulen: 1.: Zusammenhänge und Muster in der Materie, 2.: Schlussregeln und Denkgesetze sowie 3.: Gedankenbäume und -ketten, Rekursion und Induktion. Das Denken ist geradlinig, sachbezogen, strukturiert und präzise. Es geht um das Analysieren, Schließen, Lösen, Eruieren, Rechnen, Verarbeiten sowie Gedankengänge systematisch und strukturiert zu gestalten. Es besteht Interesse an Grundsätzlichkeiten, Prinzipien, Strategien, Modelle, Theorien und wichtigen Aussagen. Man muss Informationen in Einzelteile zerlegen, um sie für die Lösung in neue Einheiten zusammenzusetzen, nachdem man die Informationen sortiert und auf Wichtigkeit geprüft hat und helfende Hinweise und Tendenzen für die zukünftigen Denkprozesse abgeleitet hat. Wichtig dabei ist, sich nicht zu verzetteln und den roten Faden beizubehalten. Man muss die Gabe haben, Informationen auf sogenannte Wenn-Dann-Formeln hin zu durchleuchten, die hilfreich sein könnten für die Lösung des Problems oder die Klärung eines Sachverhaltes. Wichtig ist, dass man immer Schritt für Schritt vorgeht. Dieses Denken ist wohl die Krönung der Schöpfung der Evolution.

Ich möchte hier 10 Perlen der Mathematik erwähnen, die von großer Bedeutung sind:

01. Die Gödel'schen Unvollständigkeitssätze
Genauer werden zwei Unvollständigkeitssätze unterschieden. Der Erste Unvollständigkeitssatz besagt, dass es in hinreichend starken widerspruchsfreien Systemen immer unbeweisbare Aussagen gibt. Der Zweite Unvollständigkeitssatz besagt, dass hinreichend starke widerspruchsfreie Systeme ihre eigene Widerspruchsfreiheit nicht beweisen können.

02. Das Banach-Tarski-Paradoxon
Wenn das Auswahlaxiom gilt, dann kann eine Vollkugel so in Stücke zerlegt werden, dass dann die Teile so im Raum verschoben und anschließend gedreht werden können, dass man zusammengesetzt zwei Vollkugeln hat, die beide das gleiche Volumen haben, wie die Kugel am Anfang, die zerlegt wurde. Man hat also das Volumen verdoppelt ohne etwas hinzugetan zu haben. Es folgt also, dass man den Stücken kein Volumen zuordnen kann.

03. Der Satz von Poincaré-Perelman
Wenn ein dreidimensionaler geschlossener Raum einfach-zusammenhängend ist, dann ist dieser Raum topologisch identisch mit der dreidimensionalen Sphäre. Ein Raum ist einfach zusammenhängend, falls er wegzusammenhängend ist und sich jeder geschlossene Weg auf einen Punkt zusammenziehen lässt, d.h. nullhomotop ist. Anschaulich kann man diesen 3-dimensionalen Fall mit dem 2-dimensionalen Fall vergleichen: Wenn man auf einer geschlossenen Oberfläche eine geschlossene Kurve problemlos immer zu einem Punkt zusammenziehen kann, dann ist diese Fläche stetig in eine Kugeloberfläche deformierbar.

04. Der Satz von Fermat-Wiles
Dieser Satz sagt aus, dass die Summe zweier n-ter Potenzen beliebiger ganzer Zahlen ungleich 0 niemals gleich der n-ten Potenz irgendeiner weiteren ganzen Zahl ungleich 0 sein kann, wenn n>2 ist.

05. Der Satz von Catalan-Mihăilescu
Es wurde hier bewiesen, dass die Differenz zweier beliebiger Potenzen, gebildet aus ganzen Zahlen ungleich 0, wobei die Exponenten natürliche Zahlen echt-größer als 1 seien, mit der Ausnahme von 3 hoch 2 - 2 hoch 3 = 1, sonst niemals gleich 1 ist.

06. Die Kontinuumshypothese
Die Behauptung ist, dass es keine Menge gibt, deren Mächtigkeit zwischen der Mächtigkeit der natürlichen Zahlen und der Mächtigkeit der reellen Zahlen liegt. Es konnte bewiesen werden, dass man diese Behauptung weder beweisen noch widerlegen kann.

07. Der 4 Farben-Satz
Mit einem Computerbeweis konnte bestätigt werden, dass 4 verschiedene Farben ausreichen, um in jeder beliebigen Landkarte die Länder so zu färben, dass benachbarte Nationen verschiedene Farben haben. Für 5 Farben gibt es einen einfachen Beweis mit dem Beweisprinzip der vollständigen Induktion.

08. Der Primzahlsatz
Der Primzahlsatz sagt aus, dass die Anzahl der Primzahlen kleiner-gleich x für große x dargestellt werden kann durch: x geteilt durch den natürlichen Logarithmus von x. Daraus folgt dann, dass die Änderungsrate der Anzahl der Primzahlen kleiner-gleich x gegen 0 läuft.

09. Die Quadratur des Kreises
In der Algebra beweist man, dass man zu einem mit Zirkel und Lineal konstruierbaren Kreis mit Zirkel und Lineal nicht ein Quadrat konstruieren kann, das den gleichen Flächeninhalt hat, wie der Kreis.

10. Die Lösbarkeit von Polynomgleichungen
Für Polynomgleichungen kleiner fünften Grades gibt es Lösungsformeln. Jeder kennt z.B. die Mitternachtsformel für quadratische Gleichungen. Wenn der Grad aber mindestens 5 ist, dann gibt es dafür im Allgemeinen keine Lösungsformeln, in der Radikale vorkommen.

Da Differentialgeometrie und Algebraische Topologie meine beiden Spezialgebiete in der Mathematik sind, möchte ich drei bedeutende Klassifikationssätze von Flächen präsentieren:

Nr. 1: Einfach zusammenhängende Flächen mit konstanter Krümmung, die nicht unbedingt kompakt, aber vollständig sind, sind klassifizierbar: Durch Skalierung kann man sich auf die Krümmungen 1, 0 und -1 beschränken. Dann gibt es, bis auf Isometrie, jeweils nur eine derartige Fläche: Die Einheitssphäre, die euklidische Ebene und die hyperbolische Ebene.

Nr. 2: Jede geschlossene zusammenhängende Fläche ist homöomorph zu genau einem der drei folgenden Räume: Einer Sphäre, einer zusammenhängenden Summe von Tori und einer zusammenhängenden Summe von projektiven Ebenen.

Nr. 3: Jede 2-dimensionale, kompakte und zusammenhängende Fläche ohne Rand setzt sich zusammen aus der Sphäre, dem Torus, der Klein'schen Flasche und der Kreuzhaube.

Als nächtes möchte ich noch einen sehr tollen und wichtigen Satz, der von Carl Friedrich Gauß stammt, aus der Differentialgeometrie vorstellen:

Es sagt aus, dass die Gauß-Krümmung lokal invariant ist unter Isometrien. Anschaulich betrachtet, bedeutet das, dass die Gauß-Krümmung allein durch die Maße in der Fläche, ohne den 3-dimensionalen Raum drumherum kennen zu müssen, schon bestimmt ist. Ein Flächentier, dass in der Oberfläche lebt und nichts anderes kennt, kann also durch Messungen auf der Oberfläche herausfinden, wie groß die Gauß-Krümmung in einem Punkt ist. Sollte das Flächentier zusätzlich auch noch wissen, dass es auf einer Fläche wohnt, die orientierbar, kompakt, zusammenhängend und ohne Rand ist, wobei eine Planetenoberfläche diese Eigenschaften wohl hat, dann kann es mithilfe einer bestimmten Gauß-Bonnet-Formel wegen der Kenntnis der Gauß-Krümmung in jedem Punkt entscheiden, ob es auf einer zur Sphäre homöomorphen oder auf einer zur Sphäre mit g Henkeln homöomorphen Fläche lebt. Die Gauß-Bonnet-Formel, die das Flächentier braucht, lautet:

Dabei ist K die Gauß-Krümmung und es wird über die Oberfläche M (M wie Mannigfaltigkeit) mit den oben genannten Eigenschaften integriert.

Auch folgendes Schmuckstück möchte ich nicht unerwähnt lassen, weil besonders an dieser Stelle ein bewundernswerter Zusammenhang auf topologischer Ebene dargestellt wird:

Das Volumen der Anzahl aller Geraden, die eine Kurve in der Ebene der Länge L schneidet, ist mit Vielfachheit gezählt (je nach dem, wie oft die Gerade die Kurve schneidet) 2L.

Ein letzter Schatz noch aus der Differentialgeometrie ist der folgende Satz, der eine Aussage über Vektorfelder auf bestimmten Flächen möglich macht:

Der Index eines Vektorfeldes in einer Singularität (Nullvektor) ist die Anzahl, wie oft sich ein Vektorfeld um einen Vektor der Länge Null herumwindet. Sei eine geschlossene, orientierbare und kompakte Fläche mit nur isolierten Singularitäten gegeben. Wegen der Kompaktheit gibt es dann nur endlich viele isolierte Singularitäten. Es gilt dann, dass die Summe der Indizes in den endlich vielen isolierten Singularitäten der Fläche gleich der Euler-Charakteristik der Fläche ist. Die Euler-Charakteristik erhält man aus der Triangulierung der Fläche, indem man die Anzahl der Eckpunkte minus die Anzahl der Kanten plus die Anzahl der Flächen rechnet. Da die Euler-Charakteristik einer Kugel gleich 2 ist, folgt, dass auf der Kugel mindestens eine isolierte Singularität vorhanden sein muss. Das ist dann der sogenannte Igelsatz.

Der Film „A Beautiful Mind“ (2001) mit Russell Crowe ist wohl einer der populärsten Filme über Mathematik. Ich mag diesen Film, weil er zeigt, was ein menschliches Gehirn so alles leisten kann, wenn es besonders talentiert ist. Wenn man den Mann auf dem Bild unten rechts, der John Forbes Nash Jr. (Amerikanischer Mathematiker) verkörpern soll, mit den vielen Formeln sieht, dann versteht man schon, dass es wirklich sehr spannend sein muss in einer solchen Welt abzutauchen und sich damit zu beschäftigen. Im Bild unten links kann man sehen, wie der Analytiker Nash eine Zahlenwand analysiert, um einen sehr schwierigen Geheimcode für das amerikanische Militär zu entschlüsseln. John Forbes Nash Jr. hat trotz einer schweren Erkrankung einen sehr tiefgehenden Satz aus der Spieltheorie gefunden, bekannt als das sogenannte Nash-Gleichgewicht, wofür es dann den Nobelpreis gab. Ein tolles Video habe ich hier, das mir am Herzen liegt:

Es soll in dem Nash-Gleichgewicht möglich sein, bei Entscheidungsprozessen innerhalb einer Gruppe die Entscheidungen mit einem bestimmten Prinzip so zu fällen, dass man ein möglichst optimales Ergebnis erhält. In allen möglichen Bereichen der Wissenschaft, sogar im Militär, konnte diese tiefe Erkenntnis eine bedeutende Anwendung finden.

An dieser Stelle kommt etwas, das mir sehr wichtig ist zu zeigen:

Mein Lieblingsmathematiker ist Carl Friedrich Gauß (1777-1855), ein deutsches Mathematikgenie, geboren in Braunschweig. Dieses Genie wirkte vor allem an der Universität Göttingen; deswegen ist oben im Bild die Mathematische Fakultät, wo ich übrigens von 2005 bis 2009 studiert habe, in dieser kulturträchtigen Stadt zu sehen. Er war neben Mathematiker noch Astronom, Geodät und Physiker. Man kann ihn noch auf den 10 DM-Schein sehen, siehe unten links. Er soll von sich selbst gesagt haben, dass er eher Rechnen als Sprechen gelernt haben soll. Sein Leben lang behielt er die Gabe, selbst die kompliziertesten Rechnungen im Kopf durchzuführen. Wegen seiner überragenden wissenschaftlichen Leistungen galt er bereits zu seinen Lebzeiten als Princeps Mathematicorum („Fürst der Mathematiker; Erster unter den Mathematikern“). Trotz seines großen Talents war Carl Friedrich Gauß ein sehr bescheidener Mensch. Aus der Analysis stammt von ihm der schöne „Satz von Gauß“, den Sie unten rechts bewundern können. Dieser Integralsatz sagt anschaulich das Folgende aus: Sei ein Volumen in einem Vektorfeld im Raum gegeben. Die Quellstärke des Vektorfeldes im Volumen ist gleich dem Fluss des Vektorfeldes durch die Randfläche des Volumens.

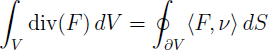Wenn ich Ihnen schon den tollen „Satz von Gauß“ gezeigt habe, möchte ich Ihnen auch gleich den ebenso tollen „Satz von Stokes“ unten präsentieren:

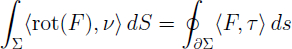
Die Anschauung dieses schönen Satzes sieht man so: Sei eine Fläche in einem Vektorfeld im Raum gegeben. Die Wirbelstärke des Vektorfeldes in der Fläche ist gleich der Arbeit durch das Vektorfeld längs der Randkurve der Fläche. Diese beiden Sätze sind eine gewisse höherdimensionale Analogie des eindimensionalen Hauptsatzes der Differential- und Integralrechnung, der relativ einfach zu beweisen ist und bereits aus der Oberstufe eines Gymnasiums bekannt sein sollte. Beide Integralsätze, Höhepunkte der Analysis 3-Vorlesung, spielen z.B. in der Elektrodynamik eine große Rolle.

Albert Einstein's Relativitätstheorie

Albert Einstein's Ergebnisse haben die Vorstellung über das Universum grundsätzlich verändert. Es kommt einer Revolution der Physik gleich. Wer hätte das gedacht, dass man sich das Universum als einen gekrümmten Raum vorstellen kann und dass Raum und Zeit miteinander verwoben sind und somit die Raum-Zeit dargestellt ist? Folgendes ist Thema in seiner sehr tollen Theorie:

- Zeitdilatation

- Längenkontraktion

- Relativistische Masse

- Äquivalenz von Masse und Energie

- Raum-Zeit-Kontinuum

Mein Lieblingskampfjet

Das ist ein sehr schönes Bild von der F/A-18 Hornet. Die Kampfjets fliegen in Formation. Aufmerksam bin ich auf diese damals in meiner Jugend geworden, als ich meine Serie „Pensacola - Flügel aus Stahl“ verfolgt habe. Es ist übrigens ein US-Kampfflugzeug, das dafür konzipiert wurde auf Flugzeugträgern zu starten und zu landen, um überall einsetzbar zu sein.

Über Jedis

Die Jedis sind Hüter des Friedens und der Gerechtigkeit; keine Soldaten. Sie sind für die Demokratie. Die Jedis dienen, anstatt zu herrschen, zum Wohle der Galaxis. Sie achten alles Leben, in jeder Form. Einem Jedi ist es nicht erlaubt eine Frau zu haben. Ergriffen vom tiefsten Ernst muss ein Jedi sein. Ein Jedi ist selbstlos, er sorgt sich nur um andere, ohne etwas als Gegenzug dafür zu verlangen. Jedis kennen keine Angst und sie haben einen Charakter, der frei ist von allem Bösen. Weil diese Friedenswächter der Galaxis Dinge sehen bevor sie passieren, meint man, sie hätten gute Reflexe. Manchmal werden sie eins mit der Macht und sind damit unsterblich. Geduld und Ruhe bewahren sie in Situationen, in denen es problematisch ist. Sie haben außerordentliche Fähigkeiten und das Lichtschwert, das die Jedis sich selbst konstruieren, ist deren Leben. Sie bleiben passiv und wenden Gewalt nur dann an, wenn es unbedingt nötig ist. Sie nutzen ihre Kraft nur zur Verteidigung und zum Schutz anderer. Ein Jedi weiß, dass er über Hass, Angst und Trauer erhaben ist. Große Erlebnisse, große Abenteuer; danach verlangt es einem Jedi nicht. Erleuchtete Wesen sind sie, nicht nur diese rohe Materie. Die Kraft eines Jedi fließt ihm durch die Macht hinzu. Abhängigkeiten meiden die Jedis, denn sie wissen, dass sie loslassen müssen von Dingen, bei denen sie Angst haben sie zu verlieren. Die Jedis streben nach Vervollkommnung durch Wissen und Ausbildung. Die Unterdrückung durch die Sith soll nie wiederkehren, darum vernichten die Jedis ohne jegliche Furcht alle Sith. Ein Jedi denkt nicht nur an die Zukunft, sondern konzentriert sich auf das hier und jetzt und lässt sich von der Macht leiten, auf dem Weg furchtlos und konsequent seinem Schicksal in der Zukunft entgegenzutreten. Im folgenden sehen Sie das Symbol für den Jedi-Orden, der seine Basis, den Jedi-Tempel, auf dem Stadtplaneten Coruscant in der „Star Wars“-Galaxis hat:

Eliteeinheit: GSG 9

So sehen die Kämpfer der Eliteeinheit GSG 9 aus. Deren Ausstrahlung ist mir irgendwie total sympathisch! Die sind für den Ernstfall wohl sehr gut gerüstet.

Die GSG 9 der Bundespolizei ist die Spezialeinheit der deutschen Bundespolizei (früher Bundesgrenzschutz) zur Bekämpfung von Schwerst- und Gewaltkriminalität sowie Terrorismus mit Standort in Sankt Augustin-Hangelar. Nach der Umbenennung des Bundesgrenzschutzes trägt die GSG 9 ihren Namen weiter, nun jedoch mit dem Zusatz „der Bundespolizei“. Die GSG 9 ist als Antiterroreinheit, zur Geiselbefreiung und Bombenentschärfung trainiert und wurde als Grenzschutzgruppe 9 am 26. September 1972 nach der Geiselnahme von München gegründet, nachdem die überforderte Polizei die Ermordung von elf israelischen Teilnehmern der Olympischen Spiele in München durch das Terrorkommando Schwarzer September nicht hatte verhindern können. Bekannt wurde die GSG 9 durch die Operation Feuerzauber in der Nacht zum 18. Oktober 1977, die Geiselbefreiung des von palästinensischen Terroristen entführten Lufthansa-Flugzeugs „Landshut“ in Mogadischu in Somalia.

Mein Sternzeichen: Waage

Wer zwischen dem 24. September und dem 23. Oktober Geburtstag hat, ist im Sternzeichen Waage geboren. Im folgenden werden wichtige Informationen über Waage-Geborene angegeben, die von wesentlicher Bedeutung sind.

Typische Eigenschaften vom Sternzeichen Waage

Stärken: anmutig, ausgewogen, ausgleichend, charmant, diplomatisch, Du-orientiert, ehrlich, friedliebend, fröhlich, geistvoll, gerecht, gesellig, harmoniebedürftig, höflich, intelligent, kontaktfähig, kultiviert, mitfühlend, optimistisch, phantasievoll, rücksichtsvoll, sensibel, schmeichelnd, sinnlich, taktvoll, umgänglich, verbindungsfähig, vermittelnd, verständnisvoll und vor allem warmherzig.

Schwächen: arrogant, bequem, eitel, empfindlich, heuchlerisch, konfliktscheu, lau, vage, leichtgläubig, oberflächlich, überangepasst, unentschlossen, verletzlich und wechselhaft.

Lebensmotto: Ich und Du! Ich gleiche aus! Ich vermittle!

Wie verhalten sich Waage-Geborene?

In diplomatischer Mission: Im Grunde genommen wünschen sich Waagen nichts außer Frieden und Harmonie. Ihre charmante und diplomatische Art lässt die Waage so manches Mal den Vermittler spielen, doch gerät sie dabei öfter auch selbst einmal zwischen die Fronten.

Künstlerisch und harmoniebedürftig: Ihre Fähigkeit, Harmonie in den Alltag zu bringen, äußert sich oft in einer künstlerischen Tätigkeit und der Scheu vor Auseinandersetzungen. Die schönen Dinge des Lebens scheinen geradezu für die Waage gemacht zu sein. Nicht aus Zufall beschäftigen sich so viele Waagen mit Kunst, Mode und Luxusartikeln.

Freundlich und stilvoll: Geschmacksfragen bereiten Waagen keine Probleme, ja es ist ihr geradezu ein Vergnügen, ein wenig Stil und Eleganz in ihren Alltag zu bringen. Die typische Waage ist freundlich und gepflegt, jedoch schwer zufriedenzustellen. Wenn sie Kritik äußert, dann allerdings stets mit einem Lächeln auf den Lippen. Die Venus verleiht der Waage ihre natürliche Freundlichkeit, die von anderen Menschen nicht immer richtig gedeutet wird. Deshalb gilt für alle Waagen: Trainieren Sie Ihre Ellenbogen und setzen Sie sich öfter durch!

Sinn für Fairness und Gerechtigkeit: Ein weiterer Charakterzug der Waage ist ihr ausgeprägter Sinn für Fairness und Gerechtigkeit. Das ist auch der Grund, warum sich die Waage für wichtige Entscheidungen viel Zeit nimmt. Sie möchte alles in Ruhe überdenken und vielleicht auch noch ein paar Meinungen einholen. Meist ist diese Taktik recht erfolgreich, doch manchmal kommt sie dadurch auch gar nicht weiter und erscheint sehr unentschlossen. Es ist eben nicht immer möglich, es allen Mitmenschen recht zu machen.

Niemanden enttäuschen: Das schroffe Neinsagen liegt der Waage nicht, sie baut in eine Absage immer ein „vielleicht“ oder „eventuell“ mit ein. Das kann aber zu Missverständnissen führen, denn nicht jeder versteht so eine subtile Absage und oftmals schürt die Waage mit ihrer diplomatischen Art ungewollt falsche Hoffnungen.

Diese Eigenschaften sind typisch für den Waage-Mann:

Die Frau, die sich einen Waage-Mann geangelt hat, kann sich wirklich glücklich schätzen. Denn er ist ein seltenes Exemplar der Gattung des Kavaliers der alten Schule. Er ist stets aufmerksam und versteht es, nette Komplimente zu machen. Da schmilzt die Frauenwelt natürlich schnell dahin. Zumal er auch mit einem sehr gepflegten Äußeren zu punkten weiß. Herr Waage ist nämlich ziemlich eitel und möchte unbedingt gefallen. Er ist ein richtiger kleiner Schwerenöter und flirtet ganz gern mal fremd. Er hat eben eine Schwäche für alles Schöne, auch für das schöne Geschlecht. Doch über ein harmloses Wortgeplänkel oder tiefe Blicke geht es zumeist nicht hinaus. Er braucht einfach das Gefühl, begehrt zu werden, das reicht ihm schon. Es fällt ihm zwar unglaublich schwer, sich festzulegen. Doch wenn er das einmal gemacht hat, ist er auch treu. Sein anfänglicher Wankelmut kann ihm im Alltagsleben allerdings des öfteren ein wenig zu schaffen machen. Er braucht jemanden, der ihm dabei hilft, sich zu entscheiden, sonst wird das nie etwas. Vor allem nicht, da er niemanden vor den Kopf stoßen möchte. Der Waage-Mann ist nämlich ungemein harmonieliebend und gibt schon mal um des lieben Friedens willen nach. Er lässt sich schnell einschüchtern, wenn andere ihre Ellenbogen ausfahren. Doch seine Anliegen setzt er trotzdem durch. Dazu braucht er keine lauten Worte, er setzt auf Diplomatie. Und darin ist er ein wahrer Meister. Er versteht es wie kein Zweiter, zwischen zerstrittenen Parteien zu vermitteln. Das macht ihn innerhalb einer Gruppe zu einem perfekten und geschätzten Teamplayer.

Ausblick

Neben ein paar Informationen über mich, z.B. über meine Logik- und IQ-Intelligenz neben wichtiger Daten zu meiner Person, werden Sie jede Menge an Bildern aus den Bereichen Mathematik, Kampfjets, Japanische Gärten und natürlich auch von mir zu sehen bekommen. Darüberhinaus habe ich noch ein paar Links zu guter Musik zusammengestellt. Ab und zu werden Sie hier, vor allem auf der Home-Seite, gewisse Videos vorfinden. Auch ein paar lesenswerte mathematische Schriften, die ich zum Teil aus dem sehr informativem Internet zusammengesammelt oder die ich selber geschrieben habe, können eingesehen werden. Für den Schachinteressierten gibt es hier ebenfalls etwas zu finden, wie z.B. eine Schachpartie zwischen dem Computer und mir. Außerdem habe ich einige Witze für eine kleine Unterhaltung aufzulisten. Ich empfehle da den letzten Witz unten über Mathematiker.

Zur Homepage

Diese Homepage ist von mir, Sven Dooley, programmiert und nach mehrfachen Aktualisierungen über einige Monate seit dem 1. Januar 2025 vollständig fertiggestellt. Gelernt habe ich HTML im Internet und so alles nach und nach zusammengebastelt. Sollten irgendwelche Beanstandungen vorhanden sein, so bitte ich mir diese per Email zu melden, damit ich korrigieren kann. Haften muss ich für eventuelle Inhalte, die nicht unbedenklich sind; daher wäre es ganz gut, wenn man mir darüber Bescheid gibt.